创建岭回归

线性回归的主要问题之一是它对异常值敏感. 在现实世界中的数据收集期间, 错误地测量输出是很常见的. 线性回归使用普通最小二乘法, 其试图最小化误差的平方. 异常值倾向于导致问题, 因为它们对总体误差有很大贡献. 这往往会扰乱整个模型.

准备

考虑以下图形:

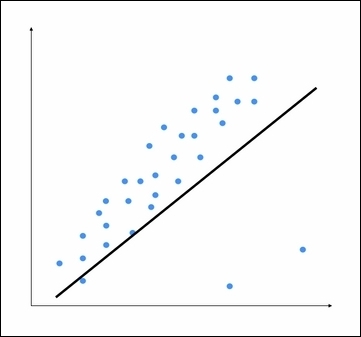
底部的两个点显然是异常值, 但这个模型试图适合所有的点. 因此, 整体模型往往不准确. 通过目视检查, 我们可以看出下图是一个更好的模型.

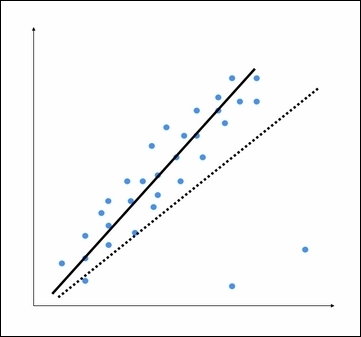
普通最小二乘法在构建模型时考虑每个数据点. 因此, 实际模型最终看起来像前面图中所示的虚线. 我们可以清楚地看到, 这个模型是次优的. 为了避免这一点, 我们使用正则化, 其中对系数的大小施加惩罚. 这种方法称为岭回归.

怎么做...?

让我们看看怎么在 python 中实现岭回归.:

• 您可以从data_multivariable.txt文件加载数据. 此文件在每行中包含多个值. 除最后一个值以外的所有值构成输入特征向量.

• 将以下行添加到regressor.py. 让我们用一些参数初始化一个岭回归

ridge_regressor = linear_model.Ridge(appha=0.01, fit_intercept=True, max_iter=10000)

• alpha参数控制复杂性. 随着α越接近0, 岭回归倾向于变得更像具有普通最小二乘的线性回归. 所以, 如果你想使其对异常值的敏感性, 你需要给alpha分配一个更高的值. 我们认为值为0.01, 这是中等的.

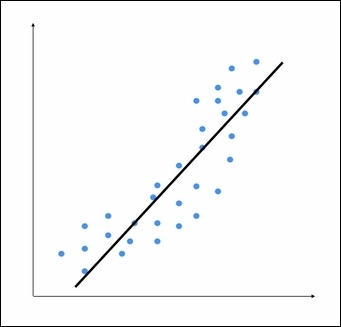
• 接下来训练岭回归

redge_regressor.fit(X_train, y_train)
y_test_pred_ridge = ridge_regressor.predict(X_test)
print ('Mean absolute error =', round(sm.mean_absolute_error(y_test, y_test_pred_ridge), 2))
print ('Mean squared error =', round(sm.mean_squared_error(y_test, y_test_pred_ridge), 2))
print ('Median absolute error =', round(sm.median_absolute_error(y_test, y_test_pred_ridge), 2))
print ('Explain variance score =', round(sm.explained_variance_score(y_test, y_test_pred_ridge), 2))
print ('R2 score =', round(sm.r2_score(y_test, y_test_pred_ridge), 2))

运行此代码以查看错误指标. 您可以构建一个线性回归来比较和对比相同数据的结果, 以查看将正则化引入模型的效果.