k最近邻是在训练数据集中使用k最近邻的算法来找到未知对象的类别. 当我们想要找到一个未知点所属的类别时, 我们找到k个最近的邻居并进行多数投票. 我们来看看如何构建这个.

怎么做...?

• 创建一个文件, 并导入相关包:

import numpy as np
import matplotlib.pyplot as plt
import matplotlib.cm as cm
from sklearn import neighbors

from utilities import load_data

• 我们将使用data_nn_classifier.txt文件输入数据. 我们加载这个输入数据:

# Load input data
input_file = 'data_nn_classifier.txt'
data = load_data(input_file)
X, y = data[:, :-1], data[:, -1].astype(np.int)

前两列包含输入数据, 最后一列包含标签. 因此, 我们将它们分成X和Y, 如前面的代码所示.

• 数据可视化:

# Plot input data
plt.figure()
plt.title('Input datapoints')
markers = '^sov<>hp'
mapper = np.array([markers[i] for i in y])
# 我们遍历所有数据点，并使用适当的标记来分隔类
for i in range(X.shape[0]):
    plt.scatter(
        X[i, 0],
        X[i, 1],
        marker=mapper[i],
        s=50,
        edgecolors='black',
        facecolors='none'
    )

• 为了构建分类器, 我们需要指定我们想要考虑的最近邻居的数量. 我们来定义这个参数:

# Number of nearest neighbors to consider
num_neighbors = 10

• 为了可视化边界, 我们需要定义一个网格并评估网格上的分类器. 我们来定义步长:

# step size of the grid
h = 0.01

• 我们现在准备建立k-最近邻居分类器. 我们来定义一下这个并训练它:

# Create a K-Neighbours Classifier model and train it
classifier = neighbors.KNeighborsClassifier(num_neighbors, weights='distance')
classifier.fit(X, y)

• 我们需要创建一个网格来绘制边界. 我们来定义一下, 如下::

# Create the mesh to plot the boundaries
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
x_grid, y_grid = np.meshgrid(
    np.arange(x_min, x_max, h),
    np.arange(y_min, y_max, h)
)

• 我们来评估所有分数的分类器输出:

# Compute the outputs for all the points on the mesh
predicted_values = classifier.predict(np.c_[x_grid.ravel(), y_grid.ravel()])

• 画图:

# Put the computed results on the map
predicted_values = predicted_values.reshape(x_grid.shape)
plt.figure()
plt.pcolormesh(x_grid, y_grid, predicted_values, cmap=cm.Pastel1)

• 现在我们绘制了彩色网格, 让我们重新绘制数据点, 看看它们在边界上的位置:

# Overlay the training points on the map
for i in range(X.shape[0]):
    plt.scatter(
        X[i, 0],
        X[i, 1],
        marker=mapper[i],
        s=50,
        edgecolors='black',
        facecolors='none'
    )

plt.xlim(x_grid.min(), x_grid.max())
plt.ylim(y_grid.min(), y_grid.max())
plt.title('k nearest neighbors classifier boundaries')

• 现在我们可以考虑一个测试数据点, 看看分类器是否正确执行. 我们来定义它并绘制它:

# Test input datapoint
test_datapoint = [4.5, 3.6]
plt.figure()
plt.title('Test datapoint')
for i in range(X.shape[0]):
    plt.scatter(
        X[i, 0],
        X[i, 1],
        marker=mapper[i],
        s=50,
        edgecolors='black',
        facecolors='none'
    )

plt.scatter(
    test_datapoint[0],
    test_datapoint[1],
    marker='x',
    linewidth=3,
    s=200,
    facecolors='black'
)

• 我们需要使用以下模型提取k个最近邻居:

# Extract k nearest neighbors
dist, indices = classifier.kneighbors(np.array(test_datapoint).reshape(1, -1))

• 我们来绘制k最近的邻居并突出显示它们:

# Plot k nearest neighbors
plt.figure()
plt.title('k nearest neighbors')

for i in indices:
    plt.scatter(
        X[i, 0],
        X[i, 1],
        marker='o',
        linewidth=3,
        s=100,
        facecolors='black'
    )

plt.scatter(
    test_datapoint[0],
    test_datapoint[1],
    marker='x',
    linewidth=3,
    s=200,
    facecolors='black'
)

for i in range(X.shape[0]):
    plt.scatter(
        X[i, 0],
        X[i, 1],
        marker=mapper[i],
        s=50,
        edgecolors='black',
        facecolors='none'
    )

print (
    "Predicted output:",
    classifier.predict(np.array(test_datapoint).reshape(1, -1))[0]
)

plt.show()

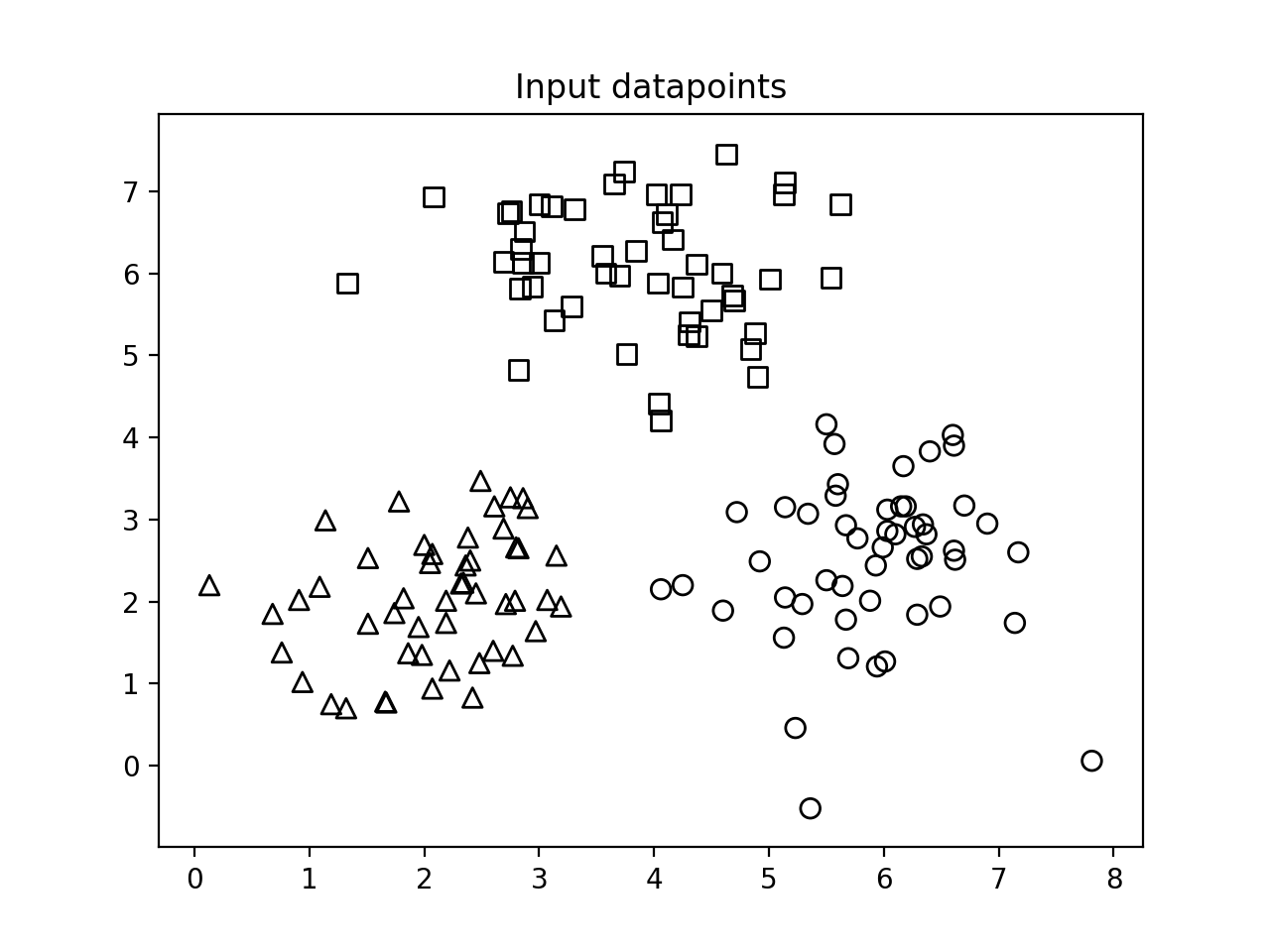
• 如果运行这个代码, 第一个输出数字描绘了输入数据点的分布:

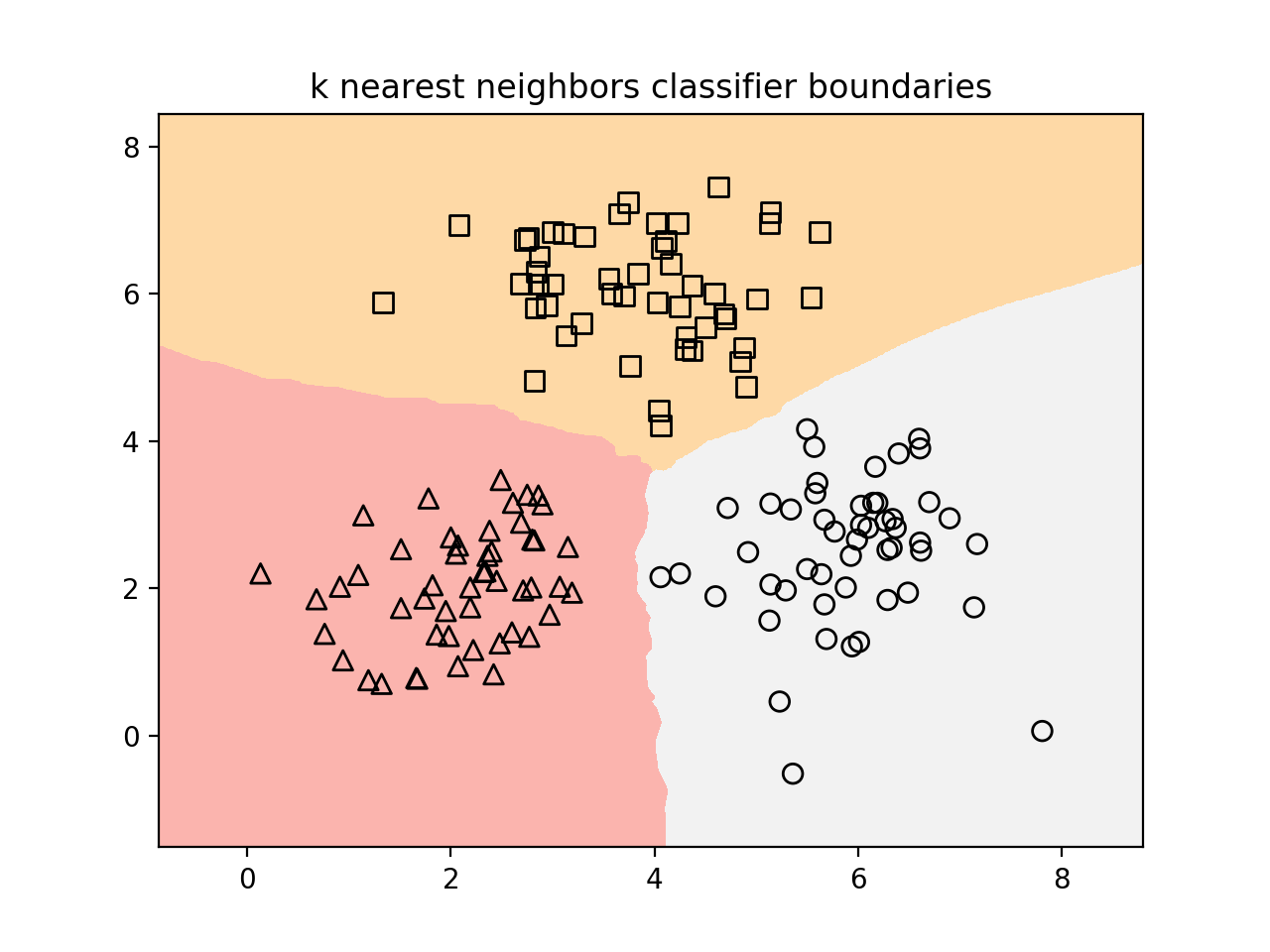
• 第二个输出图描绘了使用k-最近邻居分类器获得的边界:

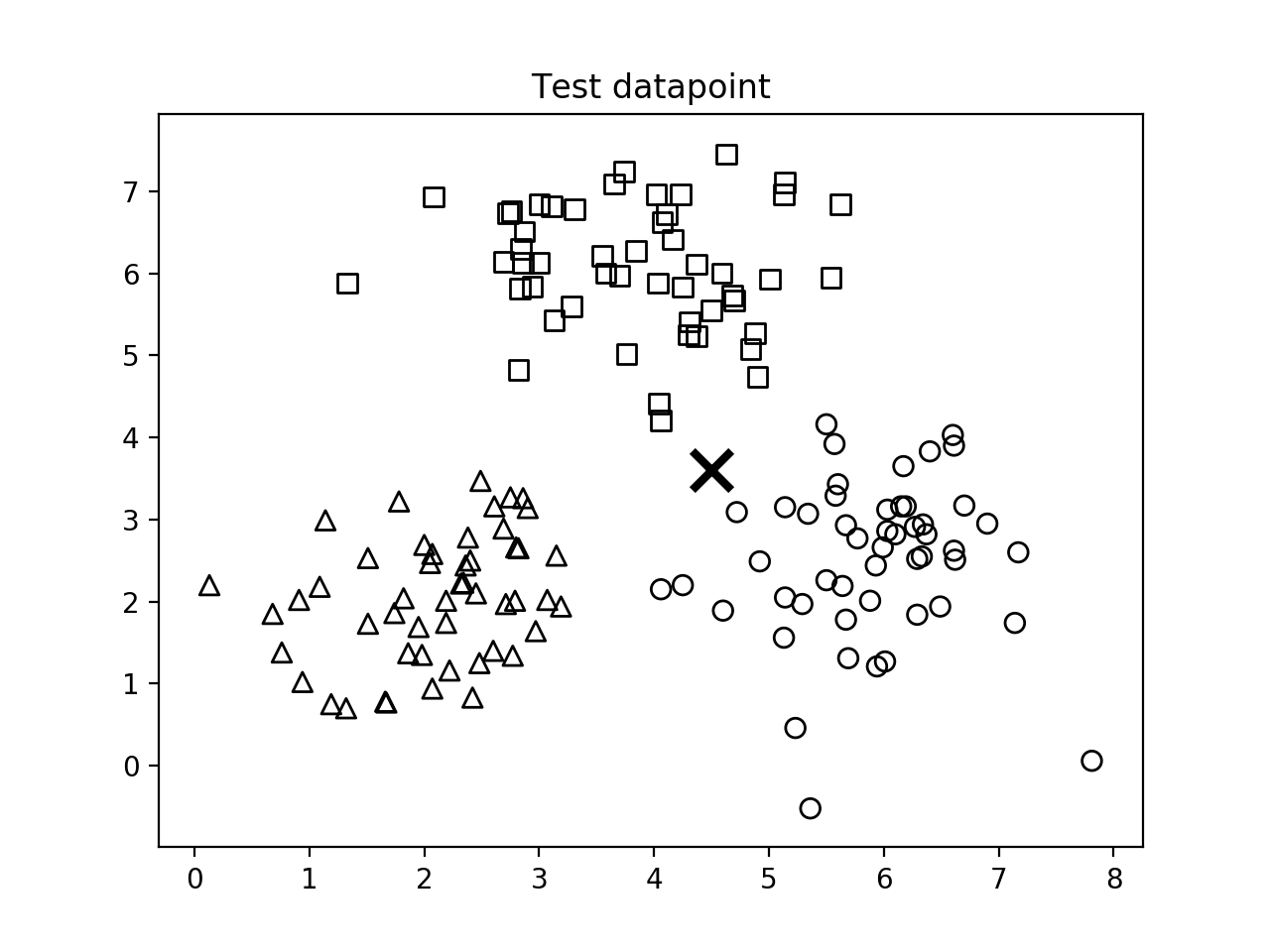
• 第三个输出图表示测试数据点的位置:

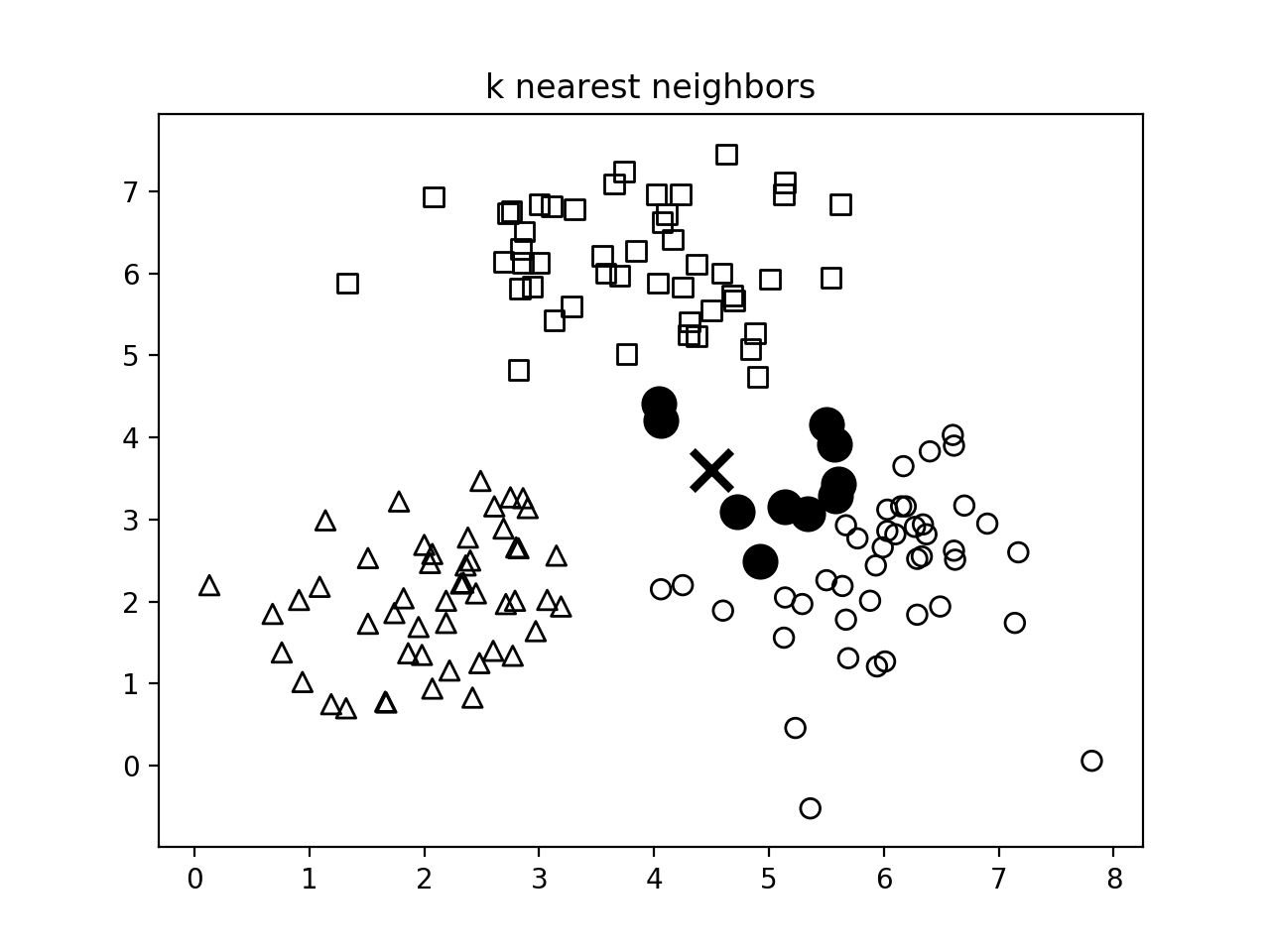
• 第四个输出数字描绘了10个最近邻居的位置:

原理...?

k-最近邻居分类器存储所有可用的数据点, 并根据相似性度量对新的数据点进行分类. 这种相似性度量通常以距离函数的形式出现. 该算法是非参数化技术, 这意味着在方法之前不需要找出任何基本参数. 我们需要做的就是选择一个适用于我们的k值.

一旦我们找到k最近的邻居, 我们就是多数票(we take a majority vote). 一个新的数据点被k个最近邻居的多数投票分类. 该数据点被分配给其k个最近邻居中最常见的类. 如果我们将k的值设置为1, 则这简单地成为最近邻分类器的情况, 其中我们将数据点分配给训练数据集中其最近邻的类. 您可以在http://www.fon.hum.uva.nl/praat/manual/kNN_classifiers_1__What_is_a_kNN_classifier_.html上了解更多信息.