多项式回归

线性回归模型的主要约束之一是它试图将线性函数拟合到输入数据. 多项式回归模型通过允许函数是多项式来克服这个问题, 从而提高模型的精度.

准备

考虑以下图形:

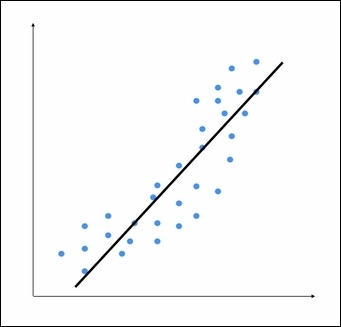
我们可以看到, 有一个数据点模式的直线. 这个线性模型无法捕捉到所有点. 让我们看看一个多项式模型是什么样子:

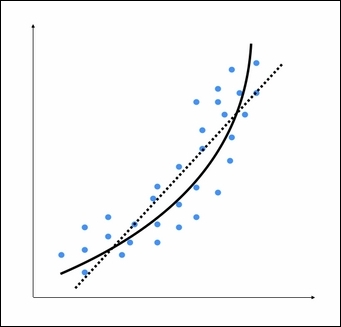
虚线表示线性回归模型, 实线表示多项式回归模型. 该模型的曲线由多项式的程度控制. 随着模型的曲率增加, 它变得更准确. 然而, 弯曲也增加了模型的复杂性, 因此, 速度更慢. 你必须要在准确性和性能方面做出折中.

怎么做...?

• 添加如下代码到regressor.py:

from sklearn.preprocessing import PolynomialFeature

polynomial = PolynomialFeature(degree=3)

• 我们初始化了一个三元多项式. 现在我们必须以多项式的系数表示数据点.

X_train_transformed = polynomial.fit_transform(X_train)
# X_train_transformed表示多项式形式的相同输入

• 让我们看看文件中的第一个数据点, 并检查它是否可以预测正确的输出.

datapoint = [[0.39, 2.78, 7.11]]
ploy_datapoint = polynomial.fit_transform(datapo)

poly_linear_model = linear_model.LinearRegression()
poly_linear_model.fit(X_train_transformed, y_train)
print ("Linear regression:", linear_regressor.predict(datapoint)[0])
print ("Polynomial regression:", poly_linear_model.predict(poly_datapoint)[0])

变量数据点中的值是输入数据文件中第一行中的值. 我们仍然在这里拟合一个线性回归模型. 唯一的区别是我们表示数据的方式. 如果运行此代码, 您将看到以下输出:

Linear regression: -11.0587294983
Polynomial regression: -10.9480782122
# 可以看到结果已经非常接近了, 如果需要更精确的, 可以调整 degree 的值

• 增大 degree 的值

polynomial = PolynomialFeatures(degree=10)

# 运行结果如下:
Polynomial regression: -8.20472183853

现在, 您可以看到预测值更接近实际输出值.