线性回归
回归是估计输入数据和连续值输出数据之间的关系的过程. 这个数据通常是实数的形式, 我们的目标是估计从输入到输出的映射的底层函数. 让我们从一个非常简单的例子开始. 考虑以下输入和输出之间的映射:
1 --> 2
3 --> 6
4.3 --> 8.6
7.1 --> 14.2
如果我要求你估计输入和输出之间的关系, 你可以通过分析模式轻松做到这一点. 我们可以看到, 在每种情况下, 输出是输入值的两倍, 因此变换函数如下:
f(x) = 2x
这是一个简单的函数, 将输入值与输出值相关联. 然而, 在现实世界中, 通常要复杂得多. 在现实世界中的功能不是那么简单!
准备
线性回归是指使用输入的线性组合来估计基础函数变量. 前面的示例是一个由一个输入变量和一个输出组成的示例变量. 考虑如下图形:
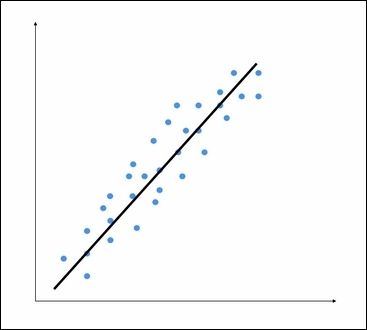
线性回归的目的是提取与输入变量相关的基本线性模型输出变量. 这旨在最小化实际输出之间的差的平方和和使用线性函数的预测输出. 这种方法称为普通最小二乘法.
你可能会说, 可能有一条弯曲的线条更适合这些点, 但线性回归不允许这样. 线性回归的主要优点是它不复杂. 如果你进行非线性回归, 你可能会得到更准确的模型, 但他们会更慢. 如图所示, 在前面的图中, 模型尝试使用直线近似输入数据点. 让我们看看如何在Python中构建一个线性回归模型.
怎么做...?
你已获得一个数据文件, 名为data_singlevar.txt. 它包含很多逗号分隔的行, 其中第一个元素是输入值, 第二个元素是输出值对应于该输入值. 你应该使用此作为输入参数:
创建名为regressor.py的文件, 并导入如下代码:
import sys import numpy as np filename = sys.argv[1] X = [] y = [] with open(filename, 'r') as f: for line in f.readlines(): xt, yt = [float(i) for i in line.split(',')] X.append(xt) y.append(yt) # 以上这段代码很简单, 这里就不做解释了- 当我们构建一个机器学习模型时, 我们需要一种方法来验证我们的模型和检查模型是否达到令人满意的水平. 为此, 我们需要分离我们的数据分为两组: 训练数据集和测试数据集. 使用训练数据集构建模型,测试数据集测试. 所以,让我们继续把这些数据分成训练和测试数据集.
# 训练/测试集 划分
num_training = int(0.8 * len(X))
num_test = len(X) - num_training
# 训练数据
X_train = np.array(X[:num_training]).reshape((num_training, 1))
y_train = np.array(y[:num_training])
# 测试数据
X_test = np.array(X[num_training:]).reshape((num_test, 1))
y_test = np.array(y[num_training:])
这里, 我们按80%测试集, 20%测试集划分.
- 下面进行训练模型的建立:
from sklearn import linear_model
# create linear regression model
linear_regressor = linear_model.Linearregresion()
# Train the model using the training sets
linear_regressor.fit(X_train, y_train)
- 我们只是基于我们的训练数据训练线性回归. fit 方法接受输入数据并训练模型. 演示如下:
import matplotlib.pyplot as plt
y_train_pred = linear_regressor.predict(X_train)
plt.figure()
plt.scatter(X_train, y_train, color='green')
plt.plot(X_train, y_train_pred color='black', linewith=4)
plt.title('Training data')
plt.show
- 现在可以运行以下代码来查看:
python regressor.py data_singlevar.txt
展示结果如下:
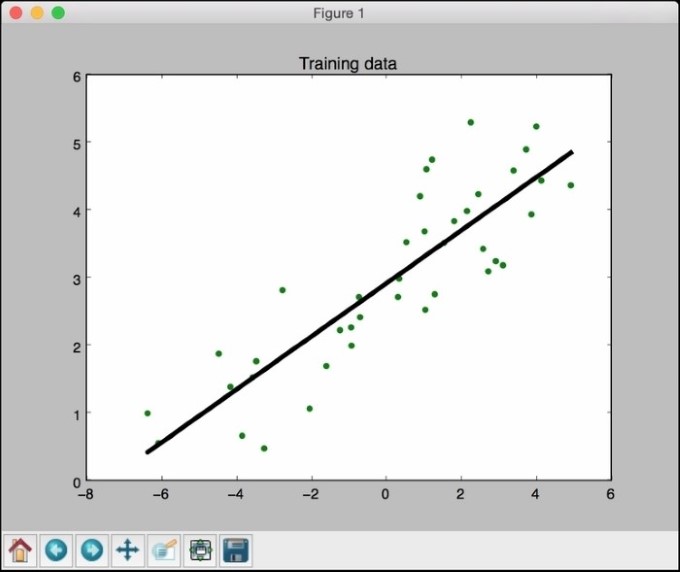
在前面的代码中, 我们使用训练模型来预测训练数据的输出. 这不会告诉我们该模型如何对未知数据执行, 因为我们在训练数据本身上运行的. 这只是给我们一个想法如何模型适合训练数据. 看起来它做好了,你可以看到在上图!
现在让我们用测试数据试试看:
Y_test_pred = linear_regressor.predict(X_test)
plt.scatter(X_test, y_test, color='green')
plt.plot(X_test, y_test_predm color='black', linewith=4)
plt.title('Test data')
plt.show()
如下图所示: